Many standard speech recognition systems train hidden Markov models (HMMs) for each phoneme whose states are modeled by a Gaussian mixture model (GMM). For the sake of simplicity each phoneme's HMM is trained with the same number of mixture components since it would be tedious to tune this manually. This is largely presumptuous, however, and it would be far safer to assume that the model for each phoneme can have a different structure from others.

The problem of finding that a sample came from component i, where i = 1, 2, 3, ..., k is best characterized by a multinomial distribution. This however, requires some sort of prior knowledge about the likelihood that each component exists. Dirichlet distributions (DDs), and by extension Dirichlet processes (DPs) act as the conjugate prior to the multinomial distribution and are therefore an excellent choice of nonparametric Bayesian approaches to find the optimal number of components.

There are many ways to interpret DPs but this work focuses entirely on the stick-breaking representation. In this depiction, a stick of unit length is broken repeatedly. Each break represents a new mixture component and the length of the broken piece is its respective weight.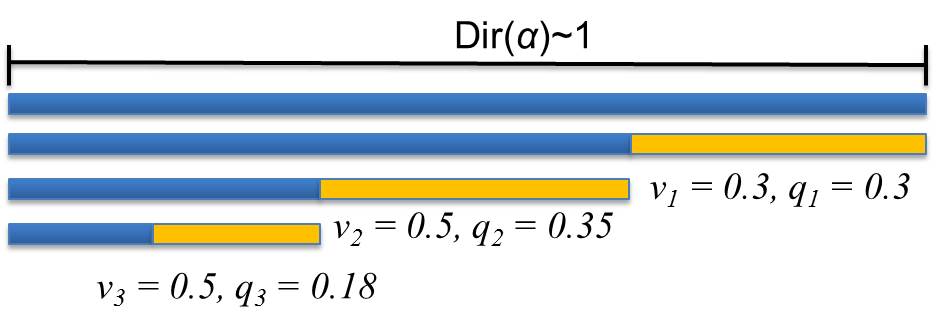


Figure 1: The stick-breaking representation of a Dirichlet distribution. Each q represents the fraction of the original whole stick (i.e. mixture weight) and each v is the fraction of the remaining stick length
In a sense, DPs are distributions over distributions, and therefore require an infinite number of parameters. This means that calculations of the posteriors are intractable, i.e. calculating a probability would require an infinite amount of time. Inference algorithms make approximations about these complex models to help simplify them so that calculating posteriors becomes analytically solvable. There are many forms of inference that can be used for this purpose, most common of which is Markov chain Monte Carlo (MCMC). MCMC takes samples of the latent variables of the distribution of interest to estimate the "true" distribution. Unfortunately, for big data problems like speech recognition, these methods require infeasible amounts of calculations. To remedy this problem, variational inference algorithms convert the sampling problem of MCMC into an optimization problem. Variational inference works by assuming that the distribution's latent variables are independent and that there is an optimal distribution q from a set Q that minimizes a cost function, i.e. Kullback-Leibler divergence. This optimal approximation can then be used to calculate posteriors analytically.

This work focuses on three such algorithms: accelerated variational Dirichlet process mixtures (AVDPM), collapsed variational stick breaking (CVSB), and collapsed Dirichlet Priors (CDP). Phoneme classification is done on the TIMIT, CALLHOME English (CH-E), and CALLHOME Mandarin (CH-M) corpora. TIMIT is a well calibrated corpus and serves as a means to confirm that the experimental setup is valid. CH-E and CH-M were selected to determine if there were any language specific artifacts that influenced classification error rates.

An HMM for monophones with 16 Gaussian mixtures is initially trained for each corpus to obtain a phoneme segmentation. 39 MFCC features are extracted for each phoneme segment and then averaged in a 3-4-3 manner (i.e. the first 30% of frames are averaged, then the middle 40%, and finally the last 30%). This keeps the number of features per phoneme segment constant despite frame duration. AVDPM, CVSB, and CDP are then used to train an acoustic model using these features. These algorithms are used to find the optimal number of mixture components, for a GMM and their respective means and covariances. Classification is then performed using maximum likelihood. The scripts used for this can be found under the Downloads tab.