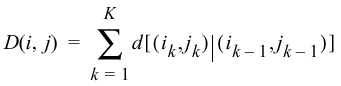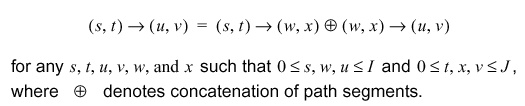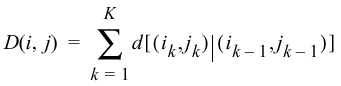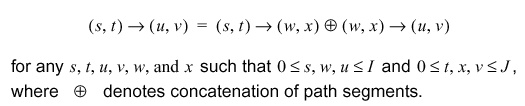BELLMAN'S PRINCIPLE OF OPTIMALITY
- Consider the discrete space (grid) shown below:
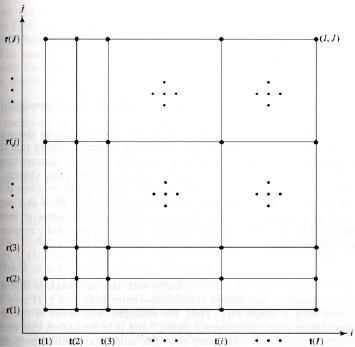
- Define a path from node (s,t) to (u,v) as an n-tuple:
(s,t), (i1,j1),
(i2,j2), ..., (u,v)
- Define a distance in moving from node
ik-1,jk-1 to ik,jk
as:
d[(ik,jk) | (ik-1,jk-1)] =
dT[(ik,jk) |
(ik-1,jk-1)] +
dN((ik,jk)
- Define an overall path cost as:
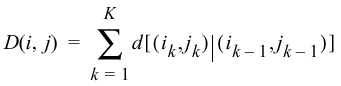
- Bellman's Principle of Optimality:
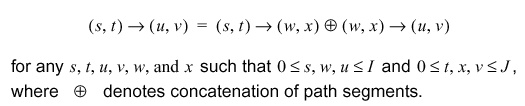
- This theorem has remarkable consequences: We do not need to exhaustively
search for the best path. Instead, we can build the best path
by considering a sequence of partial paths, and retaining the
best local path:

- The savings in computations are enormous: O(KVL) vs. O(KVL).
- For this reason, dynamic programming is one of the most widely
used algorithms in computing. It has been applied to many areas
of speech recognition including language modeling (search)
and scoring (string edits).