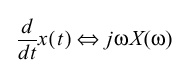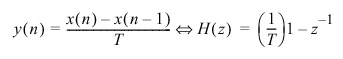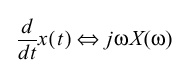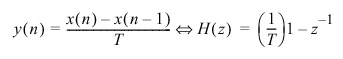ADDING TEMPORAL INFORMATION: DERIVATIVES

• We would like to add information about the change in the spectrum to our feature vector to improve our ability to distinguish between stationary sounds (vowels) and nonstationary sounds (consonants).
  
  
• Recall the definition of differentiation in the time domain:
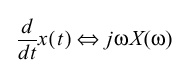
• Differentiation is an inherently noisy process since it amplifies high frequencies. Hence, we must be careful how we compute this. In practice, we use low-pass filtered derivatives (the derivative of a low-pass filtered version of the signal).
  
  
• What we really want to measure is the time derivative of the spectrum: But derivatives of continuous time signals are difficult to compute for discrete-time signals.
  
  
• Recall the definition of a derivative: This can be viewed as a digital filter: 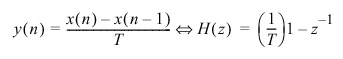Later we will explore the frequency response of this filter.
  
  
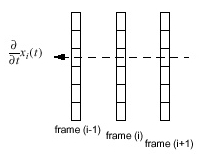
• In practice, we compute temporal derivatives of feature vectors by differentiating each element as a function of time. Since feature vectors measure the spectrum, this gives us a realistic measure of spectral change. These derivatives, called delta parameters, are concatenated with the absolute measurements to form an extended feature vector that contains absolute and rate of change information.