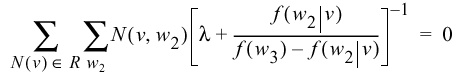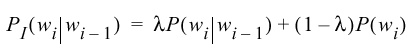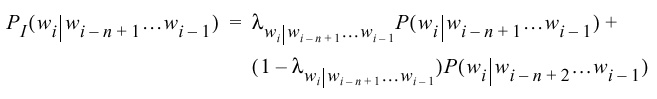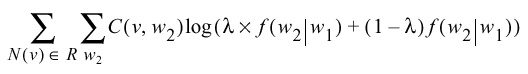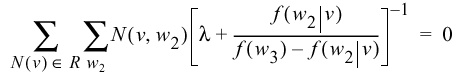DELETED INTERPOLATION SMOOTHING
- We can linearly interpolate a bigram and a unigram model as follows:
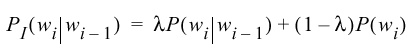
- We can generalize this to interpolating an N-gram model using
and (N-1)-gram model:
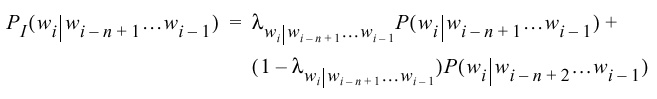
Note that this leads to a recursive procedure if the lower order
N-gram probability also doesn't exist. If necessary, everything can
be estimated in terms of a unigram model.
- A scaling factor is used to make sure that the conditional
distribution will sum to one.
- An N-gram specific weight is used. In practice, this would lead
to far too many parameters to estimate. Hence, we need to cluster
such weights (by word class perhaps), or in the extreme, use a
single weight.
- The optimal value of the interpolation weight can be found using
Baum's reestimation algorithm. However, Bahl et al suggest
a simpler procedure that produces a comparable result. We demonstrate
the procedure here for the case of a bigram laanguage model:
- Divide the total training data into kept and held-out data sets.
- Compute the relative frequency for the bigram and the unigram
from the kept data.
- Compute the count for the bigram in the held-out data set.
- Find a weight by maximizing the likelihood:
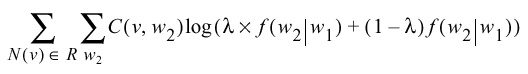
This is equivalent to solving this equation: