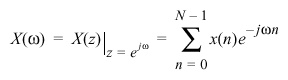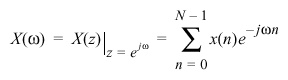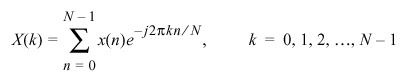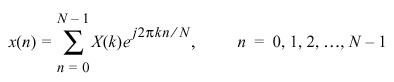DISCRETE FOURIER TRANSFORM
The Fourier transform of x(n) can be computed from the z-transform
as:
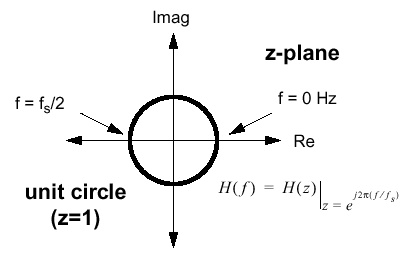
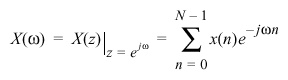 The Fourier transform may be viewed as the time-limited (finit)
z-transform evaluated around the unit circle:
The Fourier transform may be viewed as the time-limited (finit)
z-transform evaluated around the unit circle:
 The Discrete Fourier Transform (DFT) is defined as a sampled version
of the (continuous) Fourier transform shown above:
The Discrete Fourier Transform (DFT) is defined as a sampled version
of the (continuous) Fourier transform shown above:
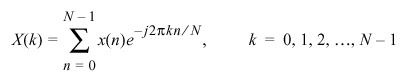 The inverse Discrete Fourier Transform (IDFT) is given by:
The inverse Discrete Fourier Transform (IDFT) is given by:
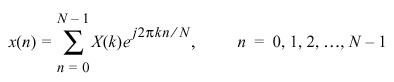 The DFT obeys the same properties one would expect for any
linear transform (linearity, superposition, duality, etc.).
The DFT obeys the same properties one would expect for any
linear transform (linearity, superposition, duality, etc.).
Note that these are not the only transforms used in speech processing
(wavelets, Wigner distributions, fractals, etc.).