Abstract
Filtering is an integral
part of signal processing. Digital filter design can prove to be
a rather arduous and cumbersome task, however, when attempted by hand.
For this reason, the use of computer programs--for not only the design
but also for the simulation and analysis of digital filters--is a valuable
and vital tool in any signal-processing application. Discussed in
this paper is a proposed header file for the most basic methods associated
with implementing a filter class in C++, along with a brief discussion
of the implementation and testing of the methods. It should be emphasized
that what is presented here is not a complete filter class, but represents
a small first step in that direction.
Introduction
The ultimate goal of
the Filter class is to design and implement linear digital filters of the
form:
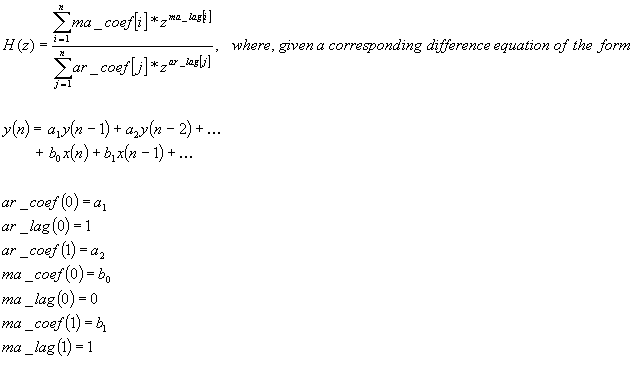
Proposed Header File
dependencies
- VectorDouble.h
- VectorFloat.h
- VectorLong.h
- external data
- filter memory
- static Boolean setDebug(Integral::DEBUG debug level)
- debug methods
- ~Filter ( )
- Filter ( )
- Filter(VectorFloat& ma_coef)
- Filter(VectorFloat& ma_coef, VectorLong& ma_lag)
- set methods
boolean setMaLag(VectorLong& ma_lag)
boolean setArCoef(VectorFloat& ar_coef)
boolean setArLag(VectorLong& ar_lag)
- get methods
boolean getMaLag(VectorLong& ma_lag)
boolean getArCoef(VectorFloat& ar_coef)
boolean getArLag(VectorLong& ar_lag)
- computational methods
Implementation
Filter filt_no_args; (1)
VectorFloat ma_coeffs(10);
Filter filt_one_arg(ma_coeffs);
(2)
VectorFloat ma_coeffs(10);
VectorLong ma_lags(10);
Filter filt_two_args(ma_coeffs,
ma_lags); (3)
The various get and set methods are for accessing and setting, respectively, the values of the filter coefficients and lags. Using filter object (3), the get and set methods could be used in the following way:
VectorFloat ar_coeffs(10);
VectorLong ar_lags(10);
ma_coeffs.assign(L"1.0,
2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0");
ma_lags.assign(L"1.0,
2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0");
ar_coeffs.assign(L"0.0,
1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0");
ar_lags.assign(L"0.0,
1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0");
// To set the coefficient
and lag values
//
filt_two_args.setMaCoef(ma_coeffs);
filt_two_args.setMaLag(ma_lags);
filt_two_args.setArCoef(ar_coeffs);
filt_two_args.setArLag(ar_lags);
// To retrieve the coefficient
and lag values
//
filt_two_args.getMaCoef(ma_coeffs);
filt_two_args.getMaLag(ma_lags);
filt_two_args.getArCoef(ar_coeffs);
filt_two_args.getArLag(ar_lags);
As it currently stands, the only method presented here that has any signal-processing pertinence at all is the apply method. Still using filt_two_args, the user should be able to use the apply method in the following way:
// declare a file object
and attach it to an input file
//
String in_filename("data.raw");
Sof in_file;
in_file.open(in_filename,
File::READ_ONLY, Sof::BINARY);
// declare the input
signal as a vector of floating-point numbers and
// have it read itself
from the input file
//
VectorFloat signal_in;
signal_in.read(in_file,
(float)0);
//
VectorFloat signal_out;
// filter the signal
//
filt_two_args.apply(signal_out,
signal_in);
It must be noted, however, that the apply method referenced in this report has not been completely tested. Please visit the ISIP website: http://www.cavs.msstate.edu/projects/speech/education/tutorials/isip_env/index.html for a working version. The methods presented here, however, will form the basis for a powerful tool which a user can employ to alleviate the complexity associated with the filter-design aspects of his/her signal processing application.
Acknowledgements